Where can you find a specific book chapter quickly? Where does Marta Muster­mann’s order go? Where can you buy the watch with the brown leather wristband? What these three questions have in common is that they all relate to a location (i.e. ‘where’) and all three assume that what is being sought exists. This is a con­cep­tu­al model that can also be applied to databases quite easily.

Let us take for example an online shop with thousands of items and customers. The data is stored in databases. The customer can search through the database for a specific item and then order it. The dis­patch­er then assigns the ordered item to the buyer with their address in­form­a­tion via the database. The process entails several searching and sorting tasks, as well as insertion and deletion op­er­a­tions during the ordering process. To manage these tasks more ef­fi­ciently, large amounts of related data are combined together in a single address position in the database. This position is cal­cu­lated using hash values and consists of a table with letter-number com­bin­a­tions that are always of the same length. Our guide will fa­mil­i­ar­ise you with the basics of using hash tables.

What is the basic idea behind a hash table?

A hash value is first cal­cu­lated from the in­form­a­tion in a data set. The hash values of all data sets in a database are located in a hash table. An ad­di­tion­al math­em­at­ic­al operation cal­cu­lates the location of the in­form­a­tion in the database from this hash value. If a user now enters a search term, this will also be turned into a hash value. The search is no longer for the 'watch with the brown leather wrist­band' but for a match between the original hash value for the item and the hash value of the search term that was just used (i.e. a match between two letter-number com­bin­a­tions). This method is used for finding highly diverse results.

Security using hash values

A hash table is created after the terms have been assigned auto­mat­ic­ally generated hash values. These are character strings that are always of the same length and are generated by a hash function. The length of the character string and the char­ac­ters contained are de­term­ined by the hash method used. They are used, for example, to secure login in­form­a­tion against attacks.

Image: Hash table in a WordPress database
In WordPress databases, the passwords of re­gistered users are stored as hash values with a length of 34 char­ac­ters. It is im­possible to convert this character string back into the cor­res­pond­ing password.

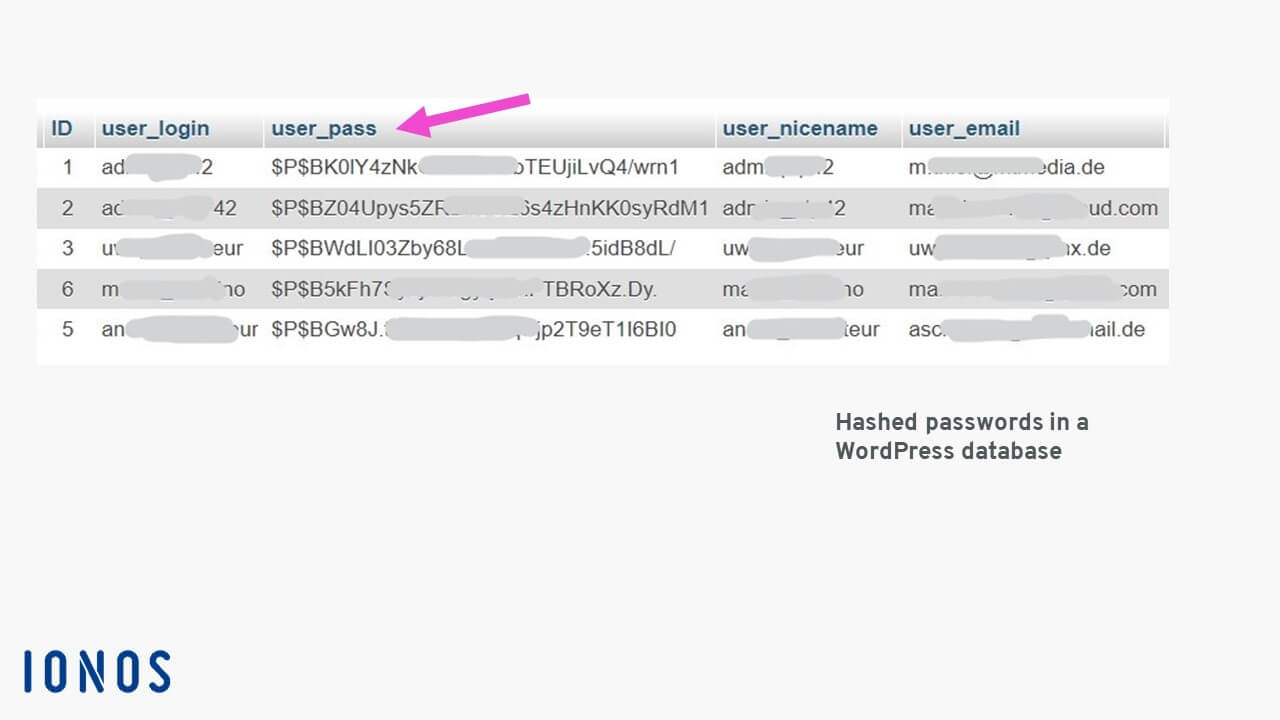
In the example of the WordPress database, when someone attempts to login, the password entered by the user is converted into a hash value using the same procedure and then compared with the entry in the 'user_pass' database field. If the two 34-character-long hash values match, access is granted. It is im­possible to convert a hash value back into a password. This is one of the quality features of a hash function.

If someone were to try to breach the security using a brute-force attack, the character string con­tain­ing all valid char­ac­ters would need to be run re­peatedly until a match was found. Even if the attacker knew the hash function that was used, it would take exactly 839,299,365,868,340,200 attempts to find a match when using uppercase and lowercase letters and numbers in a 10-character-long password.

Nav­ig­at­ing databases more quickly

Hash tables are used to speed up searches and the act of entering or deleting data sets in databases. For example, if you search a company’s employee database for a last name, this process can take a long time because each database field has to be searched one after the other (i.e. se­quen­tially) for a match. Con­vert­ing the search term into a hash value and then searching for a match in the hash table is generally much faster.

So, how is this done? Each data set is assigned a unique address. The way they are addressed is always the same within the database (e.g. 001, 002, 003 or 00A1, 00A2, 00A3, etc.). This address is cal­cu­lated using the hash function.

Let us take a look at a simple example. In this example, the database can contain 11 entries from position 0 to position 10. The name ‘Lisa’ consists of four ASCII char­ac­ters with their as­so­ci­ated ASCII codes: ‘L’ is 76, ‘I’ is 105, ‘s’ is 115 and ‘a’ is 97. You can test this yourself in Windows with the numeric keypad. For example, [Alt] + 0076 will result in ‘L’. All ASCII values are added together and result in the hash value 393 for ‘Lisa’. Adding together the ASCII values is equi­val­ent to using a hash function.

The remainder is then cal­cu­lated using whole numbers: 393 % 11 (entry locations) = 35, remainder 8 (the percent sign ‘%’ is used in many pro­gram­ming languages as the math­em­at­ic­al operator to calculate the remainder). The remainder value de­term­ines where in the database Lisa and all her other in­form­a­tion is stored – in this cal­cu­la­tion example, the index number is 8. You might imagine that with this type of ad­dress­ing, remainder values would often repeat. However, the more entry locations there are and the longer the hash value is, the less likely it is that a repeat will occur. ‘Alis Meyer’ results in a com­pletely different location despite using the same letters since the ‘A’ is now an uppercase letter and the ‘l’ is lowercase.

Image: Generating indices using a hash generator
The terms stored in the database each receive an index value which is cal­cu­lated from the hash value using a hash function. When searching for a person’s data, only the indices (001 to 363) are examined, not the entire database.

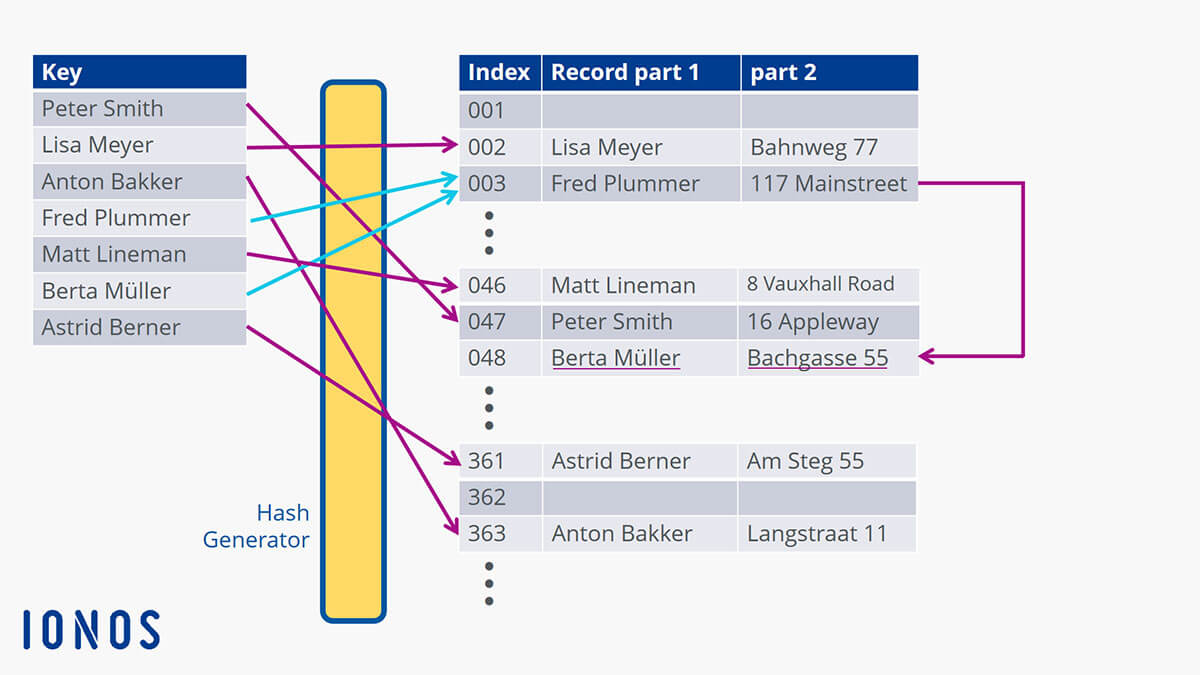
This diagram il­lus­trates the issue with repeats: Different names can be assigned the same index. This results in col­li­sions (shown by the light-blue arrows). So, what does a database ‘do’ when this kind of ‘accident’ occurs? It places the data set in the next available location in the database. If you search for ‘Berta Müller’ in the example, the search will not start at position 001. The pointer will instead start at index position 003 which will (slightly) reduce the amount of time it takes to find the name. This method is called hashing with open ad­dress­ing which then performs a linear search.

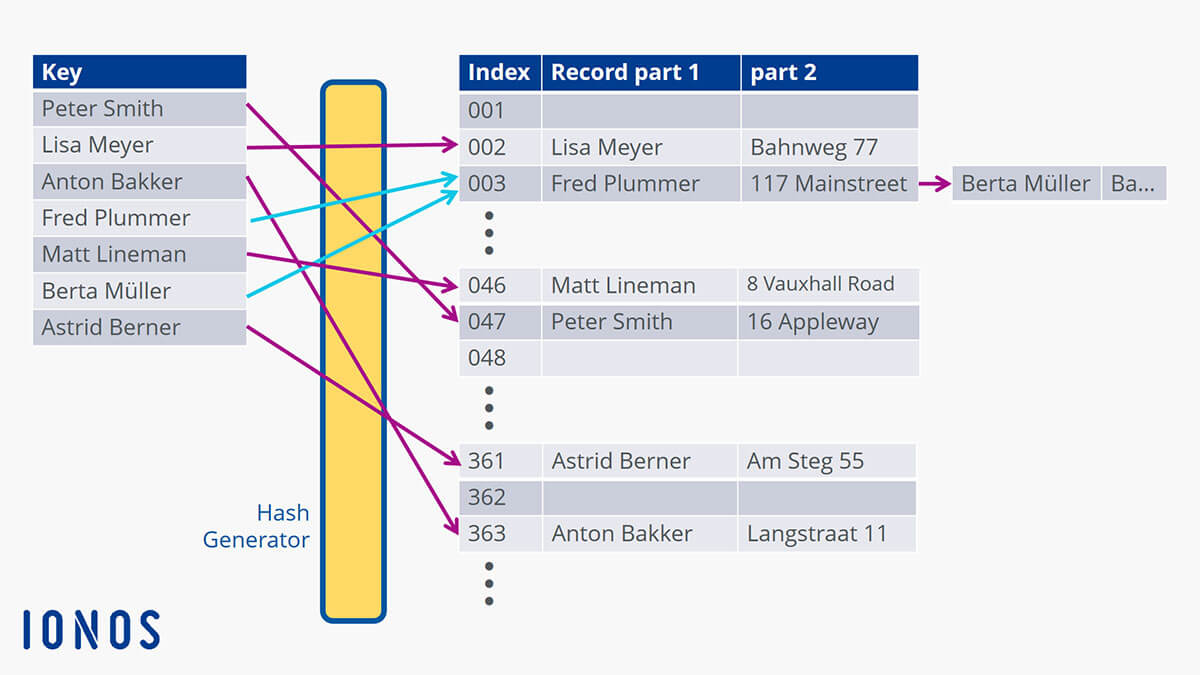
The chaining method for ad­dress­ing uses a slightly different approach. It does not create a new location for the data set. Instead, the new cor­res­pond­ing entry is linked or ‘chained’ after the first one. This means that the data set you are looking for can be found with a single search request ‘behind’ the first data set at that location. This speeds up the process.

Image: Generating indices using a hash generator: addressing with the chaining method
When using the chaining method, colliding data sets are stored under the same index one after the other (i.e. chained together).

When the search for ‘Berta Müller’ starts, the pointer is set to value 003 as cal­cu­lated from the hash table and then only has to search for the chained data set at that location. This allows large amounts of data to be packed together more ef­fi­ciently and makes it faster to search through.

This method is also used in caching so that data that has been used once can be quickly accessed again. The data is stored in the cache as a temporary storage and retrieved from there when it matches an activity-related pattern. For example, this occurs for visited websites which do not have to be com­pletely reloaded from the server when they are requested again because they can be retrieved much more quickly from the cache. Cookies also function as a form of iden­ti­fic­a­tion that can be compared against and that shows where the user has already been on the web.

What are the different kinds of hashing methods?

The hashing method just described above is also known as open or external hashing which allows data to be stored in chained lists with the­or­et­ic­ally unlimited storage space. This does not require more keys, and the chaining allows larger amounts of data to be handled. The word ‘open’ refers to open ad­dress­ing.

With closed hashing, the number of available keys is limited by the table’s capacity. If you try to store more data than its capacity allows for, overflow will occur. When running through the table again, it will be checked for available locations where the overflows can be placed.

Note

The terms ‘open’ and ‘closed’ hashing are not clearly defined. They are sometimes used with opposite meanings depending on the pub­lic­a­tion. It is thus re­com­men­ded to consult and use the cor­res­pond­ing detailed de­scrip­tion of the method in the same pub­lic­a­tion.

Cuckoo hashing is another method for avoiding col­li­sions in database tables. The term ori­gin­ates from the cuckoo’s tendency to push other birds’ eggs out of a nest to lay its own. So, in this case, two hash functions are used to describe two storage locations. If the first location is already occupied, the key stored there will be moved to a new location and the second generated key will take its place. The dis­ad­vant­age of this method is that it can result in an infinite search loop which will cause the initiated procedure to be aborted due to timeout.

There are various methods for searching databases which have been designed with com­plic­ated math­em­at­ic­al formulas that are hidden as program code on a website, such as within the basic search field with the mag­ni­fy­ing glass.

In general, databases are in­creas­ingly getting larger as the amount of data is growing at a rapid pace. Dynamic hashing addresses this issue by enlarging the hash table to avoid col­li­sions. However, this results in the hash values of pre­vi­ously stored data also changing. Special hash functions have been developed that solve this problem elegantly. There is no limit to the amount of data (at least the­or­et­ic­ally). However, searches then run less ef­fi­ciently.

Ad­vant­ages and dis­ad­vant­ages of hash tables

The biggest advantage of using a hash table is being able to search through large amounts of data quickly. However, this poses a challenge to the database’s ar­chi­tects who must estimate the required size well in advance to keep the risk of collision low. Many data types can be used in hash tables as long as hash values can be cal­cu­lated from them.

The dis­ad­vant­ages of hash tables include the fact that databases can degrade if they go through a large number of col­li­sions. The prob­ab­il­ity that a collision will occur increases with the amount of data. A large number of hash functions do not have the ability to move to the next or previous data set.

Go to Main Menu